LocalLLaMA

Github Link: https://github.com/desik1998/MathWithLLMs

Although LLMs are able to do a lot of tasks such as Coding, science etc, they often fail in doing Math tasks without a calculator (including the State of the Art Models).

Our intuition behind why models cannot do Math is because the instructions on the internet are something like a x b = c and do not follow the procedure which we humans follow when doing Math. For example when asked any human how to do 123 x 45, we follow the digit wise multiplication technique using carry, get results for each digit multiplication and then add the corresponding resulting numbers. But on the internet, we don't show the procedure to do Math and instead just right the correct value. And now given LLMs are given a x b = c, they've to reverse engineer the algorithm for multiplication.

Most of the existing Literature gives instructions to the LLM instead of showing the procedure and we think this might not be the best approach to teach LLM.

What this project does?

This project aims to prove that LLMs can learn Math when trained on a step-by-step procedural way similar to how humans do it. It also breaks the notion that LLMs cannot do Math without using calculators. For now to illustrate this, this project showcases how LLMs can learn multiplication. The rationale behind taking multiplication is that GPT-4 cannot do multiplication for >3 digit numbers. We prove that LLMs can do Math when taught using a step-by-step procedure. For example, instead of teaching LLMs multiplication like 23 * 34 = 782, we teach it multiplication similar to how we do digit-wise multiplication, get values for each digit multiplication and further add the resulting numbers to get the final result.

Instruction Tuning: We've further done finetuning on OpenAI's GPT-3.5 to teach Math.

There are close to 1300 multiplication instructions created for training and 200 for validation. The test cases were generated keeping in mind the OpenAI GPT-3.5 4096 token limit. A 5 x 5 digit multiplication can in general fit within 4096 limit but 6 x 6 cannot fit. But if one number is 6 digit, the other can be <= 4 digit and similarly if 1 number is 7 digit then the other can be <= 3 digit.

Also instead of giving * for multiplication and + for addition, different operators' <<*>> and <<<+>>> are given. The rationale behind this is, using the existing * and + for multiplication and addition might tap on the existing weights of the neural network which doesn't follow step-by-step instruction and directly give the result for multiplication in one single step.

Sample Instruction

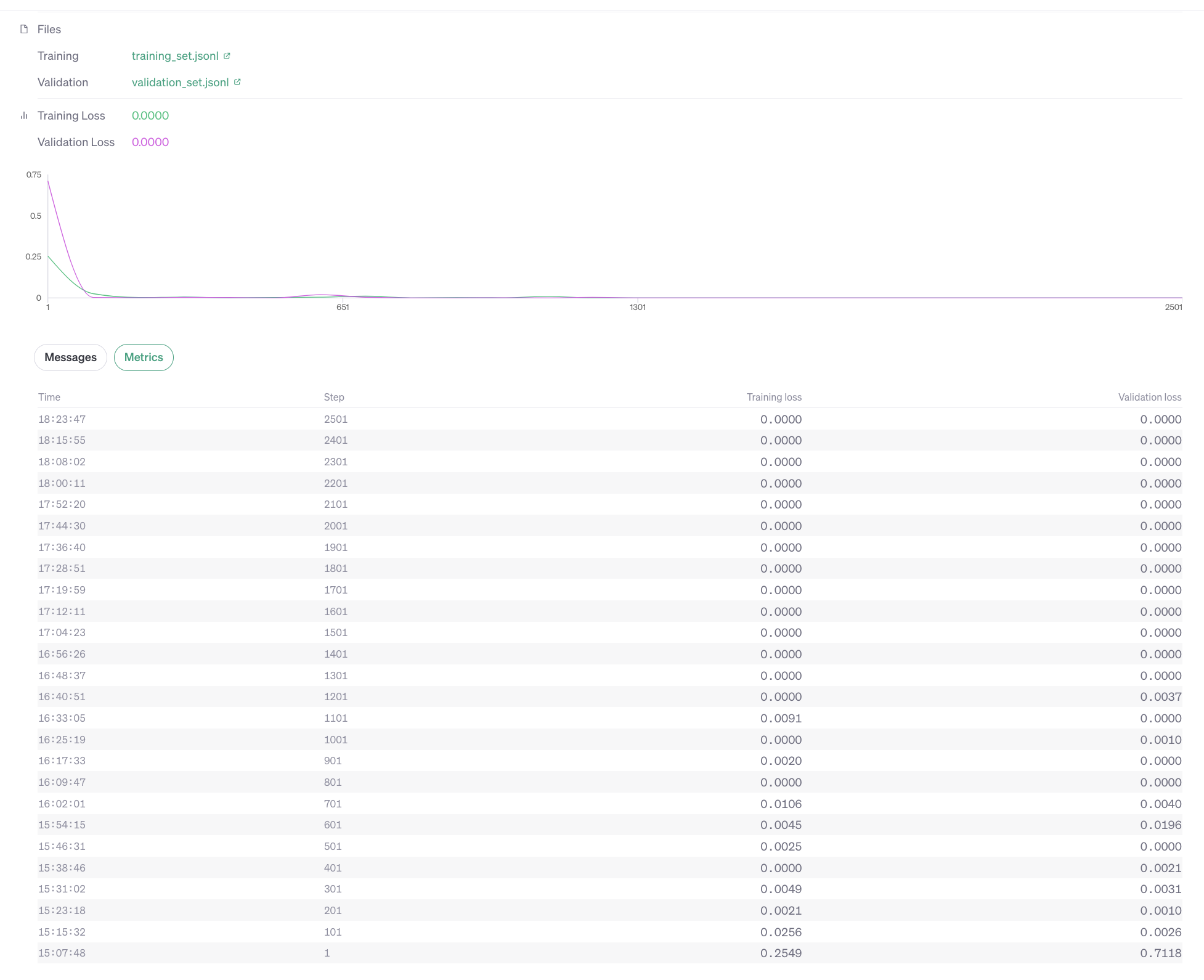
Results

The benchmarking was done on 200 test cases where each test case has two random numbers generated. For the 200 samples which were tested, excluding for 3 cases, the rest of the cases the multiplication is correct. Which means this overall accuracy is 98.5%. (We're also looking for feedback from community about how to test this better.)

Future Improvements

• Reach out to AI and open-source community to make this proposal better or identify any flaws.
• Do the same process of finetuning using open-source LLMs.
• Figure out what's the smallest LLM that can do Math accurately when trained in a procedural manner (A 10 year kid can do Math). Check this for both normal models and distilled models as well.

Requesting for Feedback from AI Community!