this post was submitted on 25 Aug 2024
579 points (98.7% liked)
Map Enthusiasts
4838 readers
125 users here now
For the map enthused!
Rules:
-
post relevant content: interesting, informative, and/or pretty maps
-
be nice
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
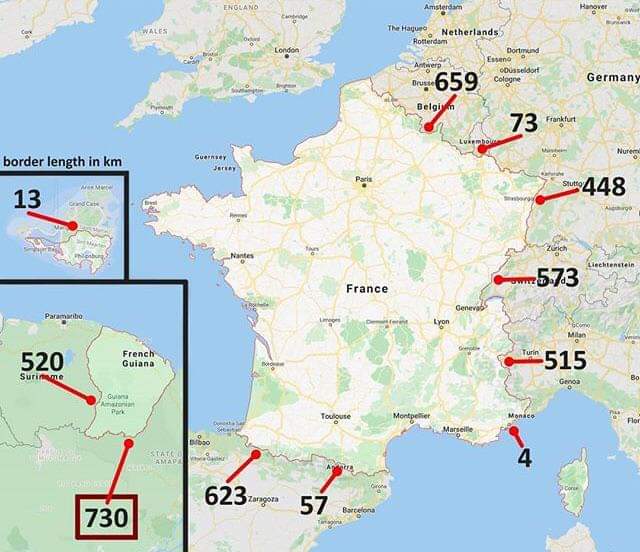
considers
Well, they aren't fractal, that's for sure.
It is true that we could make borders more-closely-map to physical features, and that would increase the length somewhat.
And we can define borders however we want, so that's up to us.
But ultimately, matter is quantum, not continuous, so if we're going to link the definition of a border to some function of physical reality, I don't think that we can make a border arbitrarily long.
Coastlines are indeed fractals, and a similar argument could be made for any border defined by natural phenomena (so like, not the long straight US/Canada border).
Coastlines are not self repeating and they are fundamentally finite.
I believe they were referring to this, where technically a coast could be seen as similar to fractals
https://en.wikipedia.org/wiki/Coastline_paradox
Literally from that page
Fractals are not necessarily self repeating, they just contain detail at arbitrarily small scales.
Which a physical space cannot fulfill
Fractals are not required to be self-repatiing. For example, the Mandelbrot set is a non-self repeating fractal pattern.
And please elaborate on how they are fundamentally finite.
Coastlines exist in the real world, they are by definition finite structures. You can only zoom in to them so far before the structure is no longer a coastline.
Thats making a lot of assumptions about quantum physics
An atom is not a coastline, even if it is a piece of one
Well, quantum mechanics is continuous, just in a way that often maps to discrete things when measured. I'm sure someone has written a research paper on quantum law, but I wonder if anyone who actually knows quantum mechanics has.
It is only continuous because it is random, so prior to making a measurement, you describe it in terms of a probability distribution called the state vector. The bits 0 and 1 are discrete, but if I said it was random and asked you to describe it, you would assign it a probability between 0 and 1, and thus it suddenly becomes continuous. (Although, in quantum mechanics, probability amplitudes are complex-valued.) The continuous nature of it is really something epistemic and not ontological. We only observe qubits as either 0 or 1, with discrete values, never anything in between the two.
Sure, but if you measure if a particle is spin up or spin down in a fixed measurement basis, physically rotate the particle, and then measure again the amplitudes change continuously. You could also measure it in another basis, which themselves form a continuous family, and get a similarly logical answer (although not independently of the first one). I don't know much about quantum field theory, but I do know that fields in it are continuous, just like they are in classical theories.
All in all, while quantum logic is part of what makes it continuous, I think I'd still stand by that it is continuous.