this post was submitted on 25 Jun 2025
165 points (94.1% liked)

Science Memes

15453 readers
2528 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

  1. Don't throw mud. Behave like an intellectual and remember the human.
  2. Keep it rooted (on topic).
  3. No spam.
  4. Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago
MODERATORS
Sal@mander.xyz
fossilesque@mander.xyz
SciBot@mander.xyz
fossilesque@lemmy.dbzer0.com
165
Jigsaw Trolley Problem (mander.xyz)
submitted 5 days ago by TauZero@mander.xyz to c/science_memes@mander.xyz
39 comments fedilink hide all child comments
 

Shamelessly stolen from you-know-where.

all 40 comments
sorted by: hot top controversial new old
[–] apotheotic@beehaw.org 8 points 3 days ago (1 children)

The ball grid problem

Albert knows that Albert doesn't know where the ball is, and also knows that Bernard doesn't know where the ball is, which means the ball is in a row where every ball has another ball in its column, which narrows it to C or D

The information that the ball must be in C or D is enough to exactly select the ball given knowledge of the column, which makes it either C3, D2 or D4

The information that Albert knows which cell it is once Albert knows that Bernard knows means that it must be C3 because if it was a D cell then Albert would still not know

C3 is the ball that was pulled from door 1, thus there was a gold ball behind door 1

Monty hall problemWhich means we dont know whether there were 6 or 3 gold behind door 1, which means its essentially a slightly different Monty Hall problem

The first door either has 2 gold balls (and 3 silver) behind it or 5 gold balls, and the second door either has 3 gold balls and 3 silver or 6 gold balls

The second door has a 66% chance of having 6 gold balls (guaranteed gold) and a 33% chance of having 3/3

The first door has a 66% chance of 2/3 and a 33% chance of 5 (guaranteed gold)

Thus door 1 has a 2/3x2/5 + 1/3 = 3/5 chance of you pulling a gold ball

Door 2 has a 2/3 + 1/3x1/2 = 5/6 chance of pulling a gold ball

You should switch doors to maximise your chance of being allowed to swap tracks

[–] TauZero@mander.xyz 2 points 3 days ago (1 children)

Knowing that the ball was gold gives you Bayesian knowledge about the boxes behind the door, since the prior probability of the host pulling a gold ball from a 6-gold door is different than from the 3/3 door. So you have to multiply Monty Hall probabilities and Bayesian probabilities together.

That assumes the host pulled a ball at random, of course, and not a deliberately gold ball.

[–] apotheotic@beehaw.org 3 points 3 days ago (1 children)

Hmm, you're quite right. My intuition is that the Bayesian portion would exactly offset the Monty hall portion. I think, at a glance, Bayes would give door 1 a 2/3 probability of having 6 gold, but Monty Hall would give door 2 the same probability, so we can effectively cancel these out and just consider a raw probability

You either have 5 gold or 2 gold 3 silver behind door 1, and 6 gold or 3 and 3 behind door 2, which gives door 2 a very slight edge. Does that check out?

[–] TauZero@mander.xyz 3 points 3 days ago (1 children)

Yes! Cancels out, leaving only a very slight edge on door 2. All that work for only... 2.77% edge over picking at random. What a troll problem, huh?

[–] apotheotic@beehaw.org 3 points 3 days ago (1 children)

Heh what a trolly problem indeed

[–] sem@lemmy.blahaj.zone 1 points 1 day ago

Speaking of trolls I assume the madman has perfect knowledge of the layout, hence did not pick a ball out at random.

[–] Etterra@discuss.online 8 points 4 days ago

I don't have that many family members, so I don't know who all those people are. Anyway I'm just gonna pick at random because I am too old and too tired for this shit.

[–] pennomi@lemmy.world 46 points 5 days ago (1 children)

Sorry fam, I don’t negotiate with game theorists.

[–] SkyezOpen@lemmy.world 17 points 5 days ago

So the only winning move is not to play? Caught you, game theorist.

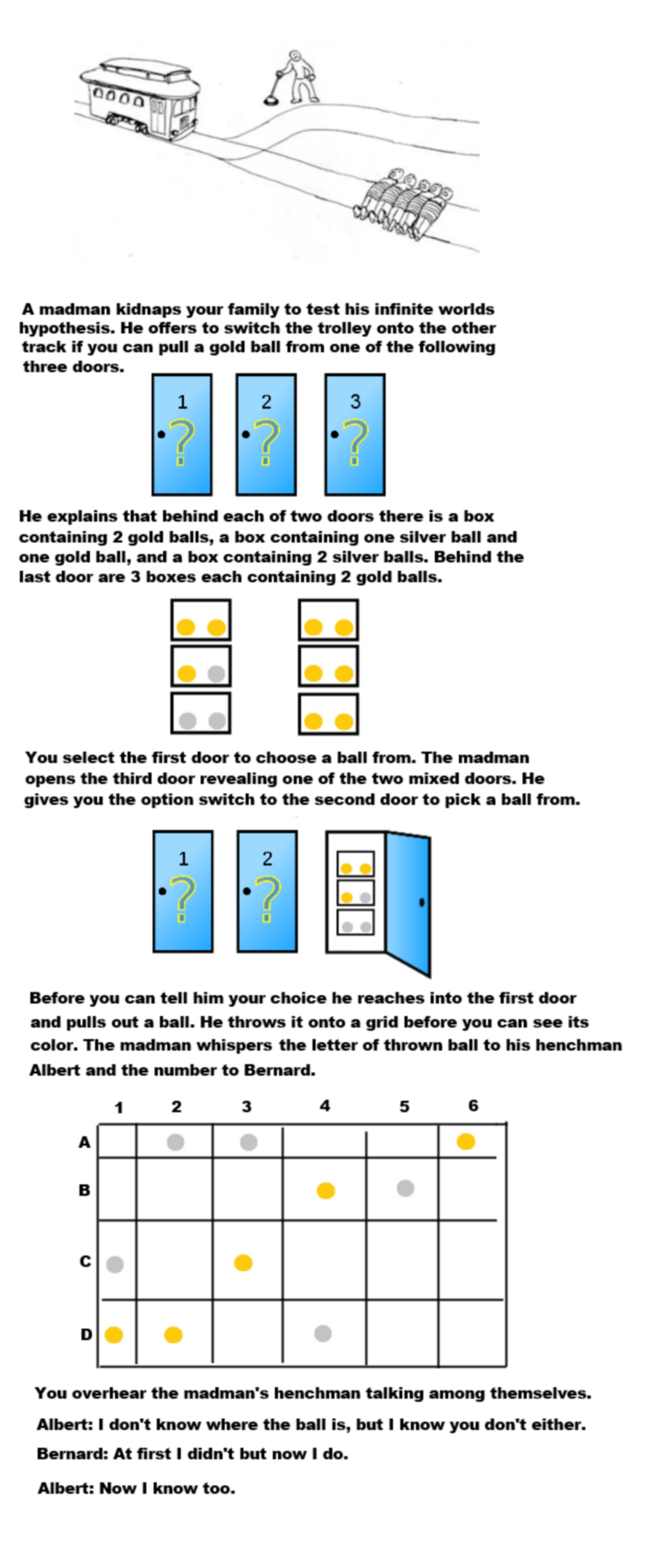
[–] Redex68@lemmy.world 32 points 5 days ago (2 children)

I think the ball is at C3.

Albert knows that Bernard doesn't know where it is exactly, that means the ball can't be in the first two rows, because if it was that would mean there's a chance for the ball to be in column 5 or 6, in which case Bernard would known right away where it is exactly (as those columns have only one ball). This means the ball must be in row C or D and column 1, 2, 3 or 4. We know Bernard was able to deduce the exact position of the ball from this information, which means it can't be column 1 (as there are 2 balls still remaining there). That means it must be in column 2, 3 or 4. We know Albert was able to deduce the exact position if the ball from this, and since row D has 2 balls still in play (collumn 2 and 4), meaning Albert wouldn't be able to guess which one it was, that means it's in row C, as row C has only one ball left in play.

Now idk what the correct choice would be statistically. If I remember correctly, the Monty Hall problem states that there's 2/3 of a chance you'll get it correctly if you switch doors, but since a gold ball was pulled out from behind the first door (the ball at C3 is gold), I think that means there's a 2/3 chance of the first door (the one from which the ball was pulled out of) being the one with all gold balls (since it contains 2/3 of all gold balls). In that case I think the probabilities cancel out? Which means it doesn't increase your chances whether you switch or not.

[–] TauZero@mander.xyz 17 points 5 days ago

Beautifully written!

I think the probabilities cancel out?

My conclusion as well. Except that since Jigsaw has taken one gold ball out, door 2 must have slightly better chance of gold ball remaining on average (75% vs 72.2%?).

[–] msage@programming.dev 1 points 3 days ago (1 children)

What I don't understand is how Albert got the information from Bernard.

Written as it is, we can deduce the C3.

But how did Albert understand from Bernards sentence that it's in the 3rd column?

[–] TheKMAP@lemmynsfw.com 1 points 3 days ago

When Albert says he knows Bernard doesn't know, he is saying that in Albert's row, every single ball has a ball below/above it. This eliminates rows A and B because if Bernard had heard 5 or six, Bernard would immediately know the exact location of the ball (but Albert is 100% sure that Bernard is confused).

This elimination of A and B is new knowledge for Bernard. He confirms that he was confused, but now he isn't. This means it's not 1 because he recently discovered that it has to be C or D, but there are balls in both C1 and D1 which means he would still be confused if that were the case.

With all this knowledge, all that's left is a row with one ball, and a row with two balls. Albert says he is not confused anymore, so it has to be the row with one ball.

[–] y0kai@lemmy.dbzer0.com 26 points 5 days ago (1 children)

I'm so confused by the added complexity here. If there's a gold ball behind every door, the choice of door doesn't matter.

We were asked to pull a ball from behind one of three doors, not figure out what two dudes know about balls in a grid.

I choose the following option:

Kick the madman in the nuts, open all the doors and take all of the balls, switch the trolly track myself, save the people, sell the balls, then go back and tie the madman to the tracks and ask him to pick the door with the black and blue balls. If he doesn't choose his own fly as the door, TROLLEY.

[–] Redex68@lemmy.world 6 points 5 days ago (1 children)

I'm think it's implied that you can only take pull out one ball at random from behind a door.

[–] y0kai@lemmy.dbzer0.com 8 points 4 days ago

We don't even get that far. Everytime we try, the dude does something before we get the chance and then changes the rules lol

[–] brisk@aussie.zone 23 points 5 days ago* (last edited 5 days ago) (2 children)

Commenting before reading other comments

Solution to grid puzzleThe henchmen's discussion implies that the letter row and number column both have at least two balls in them (required for "I don't know, but I know you don't know)". Bernard's statement to Albert makes it clear to Albert that the letter must be either row C or D depending on the number he knows.

If it was row D the answer would still be ambiguous to Bernard so it must be C3 and the ball is gold

Solution to overall puzzleI've been successfully nerd sniped and my family is dead.

[–] rooroo@feddit.org 2 points 5 days ago

I had the grid solution wrong, but your explanation is sound! Thanks!

[–] wolframhydroxide@sh.itjust.works 6 points 4 days ago* (last edited 4 days ago) (1 children)

Uh, deal? I walk up to the third door and pull a gold ball from it. I shrug at the madman.

Also, it doesn't say I can only open one box, and all three doors should still have at least one gold ball remaining.

[–] TauZero@mander.xyz 5 points 4 days ago (1 children)

Doesn't say the trolley is a runaway. Don't even need to make deals, you can safely walk away.

[–] wolframhydroxide@sh.itjust.works 5 points 4 days ago

It also doesn't say that the track isn't already headed away from the people.

[–] Rentlar@lemmy.ca 19 points 5 days ago

Hoping to select the door with a goat, that will headbutt the switch for me.

[–] hodgepodgin@lemmy.zip 11 points 5 days ago* (last edited 5 days ago) (2 children)

C3. I used to do these logic puzzles at work.

Both Albert and Bernard know the ball is at a certain row and at a certain column, respectively. Albert first admits two things:

  1. He doesn't know where the ball is. Aka, the row containing the ball has more than one ball in it. This isn't important now, but will be re-used when he asserts it again.
  2. Bernard doesn't know either. If Bernard knew where the ball was simply from the column, it'd be because that column only had one ball in it. Since he knows that Bernard doesn't know given just the row, each ball in that row is in a column that contains more than one ball.

This eliminates rows A and B, since B5 and A6 are the only balls in their columns. For this to work, Bernard now has to understand the above.

Then Bernard admits that now he knows where the ball is. Since we can eliminate or ignore each ball in A and B, it can either be balls D2, C3, and D4 and not any ball in column 1 using logic from #2.

At this point, Albert knows whether the ball is in C or D. If the madman told him the ball was in row C, then he would instantly know the ball is C3 given the elimination of C1 and D1. If he was told it was row D, then he still wouldn't know.

However, Albert admits the former, which tells us it's C3.

[–] woodenghost@hexbear.net 3 points 5 days ago* (last edited 5 days ago) (1 children)

Yes and because C3 is a golden ball, you should confidently switch to the second door. Because now it's just the Monty Hall problem with balls instead of goats. When the madman chose a door to opened, he deliberately chose a bad (mixed) door, otherwise he would have given away the correct location. The fact, that he opened the third instead of the second gives you new information, that you can take advantage of by switching, increasing your chances. Had the ball been silver, it might have been revealed to come from a bad door.

Edit: damn I just realized he picked the ball from the first door, not the second. Okay in that case we might actually have to calculate probabilities, but I'm too lazy for that.

[–] hodgepodgin@lemmy.zip 3 points 5 days ago

I have no idea what the ball thing is about. I just assumed that since he was a madman, he was just doing madman things.

[–] flora_explora@beehaw.org 1 points 5 days ago (1 children)

Thanks for the explanation, but I cannot follow on this line

Since he knows that Bernard doesn't know given just the row, each ball in that row is in a column that contains more than one ball.

Why is that? Why couldn't it be A2 or A3? In this case neither Albert nor Bertrand could tell what row/column this was either, because it would be in a row/column with another ball. How can you exclude any row with overlap with any single-ball columns?

[–] hodgepodgin@lemmy.zip 2 points 4 days ago* (last edited 4 days ago) (1 children)

It couldn't be row A or B because there would then be a possibility the ball was in A6 or B5 and that Bernard actually did know where the ball was. Albert says he knows Bernard doesn't know where the ball is, which means he is 100% confident, and the only rows that allow for that confidence are rows C and D, because each ball in each row is not alone in its column.

Scenario 1: The madman tells you the ball is in row A. Then the madman whispers the column to Bernard. Can you really be sure that Bernard knows or doesn't know where the ball is?

Scenario 2: The madman tells you the ball is in row C. From this, you can be completely sure that Bernard doesn't know where the ball is, because any column he would be given doesn't narrow it to a single row.

[–] flora_explora@beehaw.org 1 points 4 days ago

Oh of course, I didn't consider the "I know you don't either" part. Thanks, I got it now :)

[–] monk@lemmy.unboiled.info 6 points 5 days ago

I don't see no question.

[–] Dyskolos@lemmy.zip 9 points 5 days ago (1 children)

Can I try again until I get a silver ball? Please.

[–] TauZero@mander.xyz 11 points 5 days ago (1 children)

Yeah, problem doesn't specify whether you want your family to live. Common mistake.

[–] TheFogan@programming.dev 23 points 5 days ago

That's like the old joke of the CIA loyalty test.

A CIA recruit reached the final stages, at the last step he found his mother tied to a chair and gagged. His prospective boss hands him a gun and says "To prove you are ready for this job and will follow any orders, You'll need to kill your mother, I'll be outside.

10 seconds after leaving the recruiter hears the bang of a gun... followed by other bangs, clangs of metal.

Prospective recruit walks out the door.. "The god damn gun you gave me had blanks in it, so I had to beat her to death with the chair"

[–] NeatNit@discuss.tchncs.de 7 points 5 days ago (1 children)

Sounds to me like you're allowed to see the color of the ball before you take it out. This means it doesn't matter which door you open, a gold ball will be available to pull and you win. Checkmate.

[–] TauZero@mander.xyz 7 points 5 days ago (1 children)

Doesn't say it's your family tied to the tracks either.

[–] agent_nycto@lemmy.world 2 points 5 days ago (1 children)

It does in the first line?

[–] TauZero@mander.xyz 6 points 5 days ago

Your family was kidnapped and is now safely eating ice cream backstage. Tied to the tracks are 5 infinite worlds Hitlers.

[–] slippyferret@lemmy.blahaj.zone 2 points 5 days ago

Smullyan would be proud.

[–] chaos@beehaw.org 2 points 5 days ago (1 children)

I'm pretty sure the ball landed in

C3.

Albert is very sure that Bernard doesn't know either. Bernard would know the location if it was in 5 or 6, indicating to all of us that Albert was told a row that isn't A or B.

Now that Bernard can also deduce that it's not A or B, he's narrowed it down to one possibility. That means all of us now know it can't be column 1 either, because if it were, he wouldn't have gotten anything from that new fact.

Finally, now that column 1 is eliminated, Albert has deduced the location. Row D would've left two more possibilities, but row C leaves just one. Albert must know it is in row C.

For the rest, well, there isn't even actually a question, I suspect you'd open a door and pick a box and hope that you've got a gold ball to pick, and it's not clear that he's following Monty Hall rules and always opening a bad door, but I think knowing which ball got thrown would make the rest of the odds fall into place.

[–] TauZero@mander.xyz 1 points 5 days ago

it's not clear that he's following Monty Hall rules

Whenever I see a badly-specified Monty Hall Problem, I always imagine the host saying something like "Oh, you want to pick door number 1? Well, guess what - the car was behind door number 3 all along! You get nothing but a goat!" And only when you initially pick a door with the car does the host ask "Are you sure you wouldn't rather switch to door number 2? Look, there is even a goat behind door number 3!" Switching doors 100% gurantees you get a goat... or 50% silver balls in this case.